In our first part in our series “What is Spread?” we looked at the yield curve and why the BBSW and Swap curves combined makes sense as Australia’s reference curve. This week we look at what BBSW actually is, how it comes about and following on from this, what the Swap part of the equation is.
What is BBSW?
BBSW stands for ‘Bank Bill Swap Rate’. The BBSW is a compilation and average of market rates supplied by domestic banks of bank bills with specific maturities. As such it is necessary to understand what a bill of exchange is along with the market in which this class of financial instrument trades.
Bills of exchange are negotiable instruments, which trade in the money market. The money market is a wholesale short term debt market where securities with terms of less than 1 year are transacted.
Bills are known as ‘discount securities’, as when they are initially issued, the borrower, sells a bill at a discount to its face value to a lender. Bills pay no interest over the course of their life, however, the face value of the bill is returned to its holders at maturity. The difference between the face value of the bill and the price at which the bill was originally discounted is the borrowing cost to the issuer. For example, the borrower may initially receive $95, however would be required to repay the full face value of $100 at maturity rather than paying interest. This discount is how the lender makes their return.
There are various types of bills of exchange; however, it is the bank-accepted bill which forms the basis of the bank bill swap rate. A bank-accepted bill is a type of bill of exchange where a bank, for a fee, includes their name on the bill to enhance its credit worthiness; essentially, the bank takes on the primary responsibility for paying the bill’s face value to holders at maturity.
Every Sydney business day, a panel of major domestic banks provides the Australian Financial Markets Association (AFMA) with quotes on bank bills with tenors between one month and one year. AFMA then employs an averaging process to arrive at the BBSW rates, which are then published to the market just after 10am. This averaging process is to help ensure the reference rate is independent and transparent.
What is swap?
Swap contracts are probably one of the more confusing financial arrangements out in the market space, however, they needn’t be, and as a matter of fact, they are fairly straight forward when you break them down.
So what is a swap? Well as the name implies, you are swapping something: cashflow profiles. In the case of a fixed for floating swap, which is what we will be discussing here, two parties agree with one another to exchange interest payments: one fixed for one floating.
Why would investors do this? The main reasons are to hedge interest rate risk, and to engage in interest rate speculation, for example:
- An investor might have a floating rate loan, but receive income based on a fixed rate; this leaves them exposed to movements in interest rates hence they may wish to hedge this risk. They would hedge this risk by entering into a swap where they receive floating from the other party (and thus match it with their floating rate loan) and pay a fixed rate to that same party. The reverse of this could also be true (i.e. have a fixed rate loan, but receive floating revenues)
- A speculator may think that interest rates will be lower than the current market’s expectations; hence, for speculative purposes they might wish to enter into a contract where they receive fixed and pay floating, thus gaining a profit if their expectations turn out to be correct
How a swap physically works:
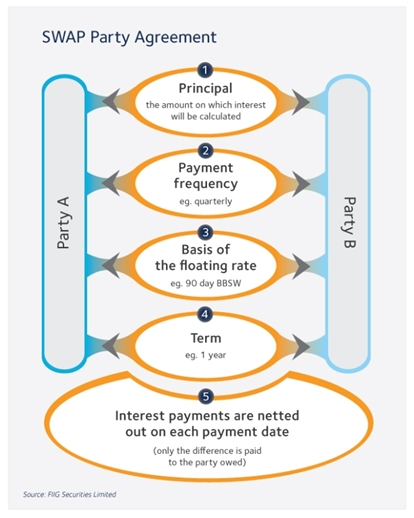
Neither party should receive an immediate gain or loss for entering this contract (as otherwise who would ever enter into the losing leg of the swap). Thus, the present value (PV) of the fixed cash flows needs to equal the present value of the expected floating rate cash flows to induce either party to contract with one another.
Looking at it differently, the quoted swap rate is the rate at which an investor is theoretically indifferent between receiving or paying fixed or floating over the length of the agreement.
Whilst this basic description of what a Swap is may be enough for most of our readers, we have included in the appendix below the mathematical formula upon which it is based.
Different yield curves
Last week we looked at the ‘normal yield curve’ and gave some reasons for its ‘normal’ shape. Although the normal yield curve is the most prevalent yield curve shape, there are variations such as the inverted yield curve, as shown in Figure 1 below.
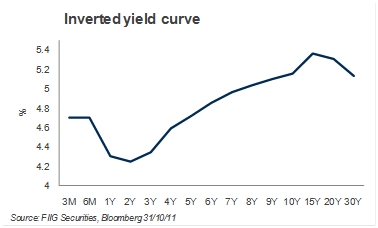
So why does this happen? There are a number of competing theories that attempt to explain yield curve shapes (including expectations theory, liquidity preference theory and market segmentation theory) however a detailed explanation of the economic theories is beyond the scope of what we are trying to do here.
When we explained the normal yield curve shape last week, we employed the liquidity preference theory. The liquidity preference theory accounts for market interest expectations and imbeds a premium for uncertainty around these expectations. The further you go out in forecasts, the more uncertainty, and thus the larger the uncertainty premium. This helps form the upward shape of the normal curve.
However, in the current market, the expectation is for lower interest rates over the next couple of years. This prevailing expectation is strong enough, and the expectations low enough, that it more than offsets the uncertainty premium causing a dip, or ‘inversion’. This gives us the ‘inverted yield curve’ shown above.
In next weeks’ article we will put the finishing touches on the theory behind what is a spread.
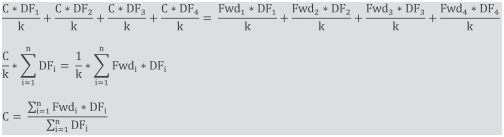
Appendix – Calculating swap
If you think of the cash flows as an investment in two bonds, one fixed and one floating, with exactly one year to maturity, then the following equality would need to be fulfilled:

Where
C=the annualised Fixed Coupon Rate multiplied by the face value
DFi=the ith discount factor
k=the Coupon Frequency
FV=the Face Value Invested; let us assume this value is 1

Where
Fwd(i)=the ith Floating Rate Coupon (annualised) multiplied by the face value
PV of the fixed leg=PV of the floating leg